Table of Contents

• Turning real fungi into cyberfungi
• Fungal dynamics: how real fungi grow
• Overview of the Neighbour-Sensing model without the maths
• Mathematical description of the Neighbour-Sensing Model
• Experimental use of the model
• Liam McNulty’s Guide
• Some examples we prepared earlier
• Modelling gravitropism
• Neighbour-Sensing documentation
• Downloads page

David Moore introduces the experimental use of the model

The Neighbour-Sensing model is an experimental tool to study how fungi grow in the real world by providing us with such a realistic computer simulation that factors affecting fungal growth can be studied in computer-time rather than real time.

It is not a game or a painting program. Rather, it provides the user with a way of experimenting with features that may regulate hyphal growth patterns to arrive at suggestions that could be tested with live fungi. The potential value of the computer simulation being that it allows the cybermycologist to carry out many more experiments than could be achieved with living fungi, and on a wider range of features.

It's not just a matter of experimental time or space, of course. Because if the model can produce simulations that are totally life-like, it also gives you the opportunity to experiment with many features (all of those in its parameter set) that are not directly accessible to the experimental mycologist who is limited to living fungi.

Initial experiments show that a random growth and branching model (i.e. one that does not include the local hyphal tip density field effect) is sufficient to form a spherical colony. The colony formed by such a model is more densely branched in the centre and sparser at the border; a feature observed in some living mycelia. Our conclusion is that no specific control is necessary to form a spherical colony - the shape is reached by the overwhelming majority of parameter settings.

Models incorporating local hyphal tip density field to affect patterning produced the most regular spherical colonies. As with the random growth models, making branching sensitive to the number of neighbouring tips forms a colony in which a near uniformly dense, essentially spherical, core is surrounded by a thin layer of slightly less dense mycelium.

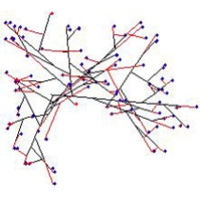
For experiments examining how to produce different branching patterns we used the branching types discussed by Nils Fries in 1943 as our paradigm, because the Friesian interpretation of fungi was enshrined in the very bedrock of fungal biology so many years ago.

A	B	C
Three different types of young colonies as described and illustrated by Fries (1943) are shown above, and are compared with visualisations produced by the Neighbour-Sensing computer model (below). The figures above were scanned from the original 1943 publication [Fries, N. (1943). Untersuchungen über Sporenkeimung und Mycelentwicklung bodenbewohneneder Hymenomyceten. Symbolae Botanicae Upsaliensis, 6(4): 633-664]; they show recently-germinated spores ('sporelings') described by Fries as: A, the Boletus type; B, the Amanita rubescens type; and C, the Tricholoma type. The corresponding simulations illustrated below were generated by the Neighbour-Sensing program using parameter sets discussed in the text.

The morphology of virtual colonies produced when branching (but not growth vector) was made sensitive to the number of neighbouring tips was closest to what Fries called the Boletus type.

This suggests that the Boletus type branching strategy does not use tropic reactions to determine patterning, nor some pre-defined branching algorithm. Following Occam’s rule that a simpler model must be preferred if it explains the experimental data equally well, we conclude that hyphal tropisms are not always required to explain “circular” (= spherical) mycelia.

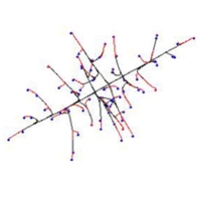
When our model implements the negative autotropism of hyphae, a spherical, nearly uniformly-dense colony is also formed, but branching is still regulated by the number of neighbouring tips (not by the density field). However the structure of such a colony is different from the previously mentioned Boletus type, being more similar to the Amanita rubescens type, characterised by a certain degree of differentiation between hyphae.

First rank hyphae tend to grow away from the centre of the colony; second rank hyphae grow less regularly, and fill-in the remaining space. In the early stages of development such a colony is more star-like than spherical. We wish to emphasise that this remarkable differentiation of hyphae emerges in the visualisation even though the program settings used do not include routines implementing differences in hyphal behaviour. In the mathematical model all virtual hyphae are driven by the same algorithm. By altering the persistence factor, it is possible to generate the whole range of intermediate forms between Boletus and Amanita types.

Finally, when both autotropic reaction and branching are regulated by the hyphal density field, a spherical, uniformly dense colony is also formed. However, the structure is different again, such a colony being similar to the Tricholoma type illustrated by Fries (illustrated above). This type has the appearance of a dichotomous branching pattern, but it is not a true dichotomy. Rather, the new branch, being very close to its parent, generates a strong density field that turns the older tip. In the previous model a tip nearby has no stronger effect than a more distant tip as long as they are both closer than R.

Hence, experimentation with the Neighbour-Sensing model allows us to suggest that the Amanita rubescens and Tricholoma branching strategies may be based on a negative autotropic reaction of the growing hyphae while the Boletus strategy may be based on the absence of such a reaction, relying only on density-dependent branching.

Differences between Amanita and Tricholoma in the way that the growing tip senses its neighbours may be obscured in life. In Amanita and Boletus types, the tip may sense the number of other tips in its immediate surroundings. In the Tricholoma type, the tip may sense all other parts of the mycelium, but the local segments have the greatest impact.

These simple initial experiments with our model show that the broadly different types of branching observed in the fungal mycelium are likely to be based on differential expression of relatively simple control mechanisms.

We presume that the 'rules' governing branch patterning (that is, the mechanisms causing the patterning) are likely to change in the life of a mycelium, as both intracellular and extracellular conditions alter. We have imitated some of these changes by making alterations to particular model parameters during the course of a simulation.

Some of the results show that the Neighbour-Sensing model is capable of generating a range of morphologies in its virtual mycelia which are reminiscent of real live fungal tissues.

These experiments make it evident that it is not necessary to impose complex spatial controls over development of the mycelium to achieve particular geometrical forms.

Rather, geometrical form of the mycelium emerges as a consequence of the operation of specific locally-effective hyphal tip interactions. We hope that further experimentation with the model will enable us to predict how tissue branching patterns are established in real life.

What is outlined above is an enlightening insight into the effectiveness of fungal filamentous hyphal growth as an evolutionary strategy. Of course we are interested in the ways that fungal mycelia grow, but this tells us about only a small part of the full range of abilities of this growth form. In many respects the mycelium is the least interesting growth form. It is the ‘default’ growth mode of the fungal cell and any changes that occur in it are imposed by external forces (nutrients, environmental conditions, etc).

Of much greater biological interest is the way in which this ‘default’ growth mode might be altered by internal (that is, self-imposed) controls to generate the numerous differentiated cells that hyphae can produce and the native interactions between hyphae that cause them to co-operate and co-ordinate in the morphogenesis of multicellular fungal tissues.

There are fundamental differences between the 'crown group' of three Kingdoms of eukaryotes (fungi, plants, and animals) in the way that the morphology of multicellular structures is determined. A characteristic of animal embryology is the movement of cells and cell populations. In contrast, plant morphogenesis depends upon control of the orientation and position of the daughter cell wall, which forms at the equator of the mitotic division spindle.

Fungi also have walls, like plants, but their basic structural unit, the hypha, exhibits two features which cause fungal morphogenesis to be totally different from plant morphogenesis. These are that:

• hyphae extend only at their apex, and
• cross walls form only at right angles to the long axis of the hypha.

A consequence of these 'rules' is that fungal morphogenesis depends on the placement of hyphal branches. Increasing the number of growing tips by hyphal branching is the equivalent of cell proliferation in animals and plants. To proliferate, the hypha must branch, and to form an organised tissue the position of branch emergence and its direction of growth must be controlled.

Another way in which fungal morphogenesis differs from that in other organisms is that there are no lateral contacts between fungal hyphae. Nothing analogous to the plasmodesmata, gap junctions and cell processes that interconnect neighbouring cells in plant and animal tissues has ever been found. The absence of lateral contacts suggests that any morphogens used to regulate development in fungi will be communicated through the extracellular environment.

Since published kinetic analyses deal exclusively with external influences (like nutrient status, culture conditions, etc.) on growth and branching kinetics, this encourages our view that a mathematical description of fungal vegetative growth might be generalised into predictive simulations of tissue formation, leading to better understanding of the parameters that generate specific morphologies.

Construction of fungal tissues

We will give you an idea of what we mean by the phrase 'fungal tissues' briefly in the rest of this page. If you haven't already done so, you need to refer to the section of this website that hosts our 21st Century Guidebook to Fungi to get the full story. [Try the hyperlinks in the next information box (they will each open in a new window)].

Development of any multicellular structure in fungi requires modification of the normal growth pattern of a vegetative mycelium so that hyphae no longer characteristically diverge, but grow towards one another to co-operate in forming the differentiating organ. The hyphal tip is an invasive, migratory structure. Its direction of growth after initial branch emergence must be under precise control as it determines the nature and relationships of the cells the hyphal branches will form.

Fungi produce several types of linear organs (strands, rhizomorphs and fruit body stems or stipes). Formation of parallel aggregates of hyphae (as in mycelial strands and cords) is common as they provide the main translocation routes for the mycelium. They are formed in mushroom cultures to channel nutrients towards developing fruit bodies; they are also formed by mycorrhizal fungi, gathering nutrients for the host plant.

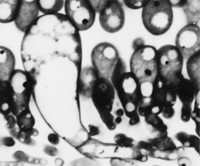
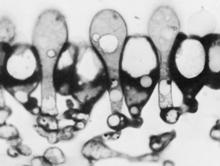
Some fungi produce rhizomorphs, which have highly differentiated tissues and show extreme apical dominance. There is often a gradation of increasing differentiation between strand, cord (or rhizomorphs) and fruit body stipe (also called the stem). Linear organs arise when young branches adhere to, and grow over, an older leading hypha. From the beginning, some of the hyphae may expand to become wide-diameter but thin-walled hyphae, whilst narrow hyphal branches (‘tendril’ hyphae) intertwine around the inflated hyphae (Figure 1).

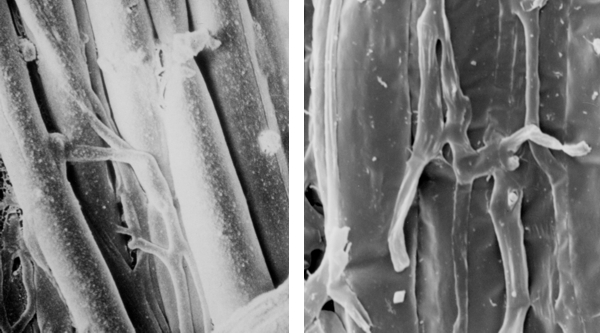Figure 1. Two scanning electron micrographs of wide and narrow hyphae intertwined in the stem tissues of the small field mushroom, Coprinopsis cinerea. Presumably this pattern of growth is produced by positive autotropisms which ensure that the hyphae initially grow parallel with one another, and other tropisms that allow the narrow hyphae to grow around and intermingle with inflated hyphae. Of course, there must also be some differentiation control that causes some (but not all) hyphae to expand to become wide diameter hyphae.

Among globose structures produced by fungi we would include sclerotia and fruit bodies. Sclerotia are tuber-like, with concentric zones of tissue forming an outer rind and inner medulla, with a cortex sometimes between them. They pass through a period of dormancy before utilizing accumulated nutrient reserves to ‘germinate’, often producing fruit bodies immediately.

Fruit bodies are responsible for producing and distributing spores, which are formed following meiosis. In Ascomycota (informally called ascomycetes), the sexually produced ascospores (contained in their asci, the cells in which meiosis took place) are enclosed in an aggregation of hyphae termed an ascoma. Ascomata (this is the plural form of 'ascoma') are formed from sterile hyphae surrounding the developing asci, and occur in nature in forms such as truffles and morels.

The fruit-bodies of Basidiomycota (commonly called basidiomycetes), the mushrooms, toadstools, bracket fungi, puff-balls, stinkhorns, bird’s nest fungi, etc., are all examples of basidiomata which bear the sexually produced basidiospores on basidia (the cells in which meiosis took place) in the spore-bearing hymenial layers. These hymenia are constructed from branches of determinate growth in a precise spatial and temporal arrangement.

A hyphal tip in the ‘embryonic’ protohymenium has a low probability of becoming a cystidium. Cystidia are large, inflated cells which are readily seen in microscope sections. When a cystidium arises, it inhibits formation of further cystidia in the same hymenium within a radius of about 30 μm. As a result, only about 8% of the hymenial hyphal branches actually become cystidia; the rest become basidia, which proceed to karyogamy and initiate the meiotic cycle (which ends with sporulation) (Figure 2). The distribution pattern of cystidia is consistent with an activator-inhibitor model that suggests that an activator autocatalyses its own synthesis, and interacts with an inhibitor that inhibits synthesis of the activator.

Sterile packing cells, called paraphyses, then arise as branches of sub-basidial cells and insert into the hymenium (Figure 3). About 75% of the paraphysis population is inserted before the end of meiosis, the rest insert at later stages of development. There is, therefore, a defined temporal sequence: probasidia and cystidia appear first and then paraphyses arise as branches from sub-basidial cells. Another cell type, cystesia (adhesive cells), differentiate when a cystidium grows across the gill space and contacts the opposing hymenium (this contact has just been made by the cystidium shown in Figure 2).

Although attempts have been made in the past to produce mathematical models that describe apical growth in three dimensions, we are not aware of any kinetic analysis of fungal mycelial growth in three dimensions that might contribute to understanding fungal tissue morphogenesis.

It is certain, though, that the equation Ē = µ_max G (Equation 1) [where Ē is the mean extension rate of the colony margin; µ_max is the maximum specific (biomass) growth rate; and G is the hyphal growth unit length] is fundamental to understanding branching kinetics.

The ratio E/μ can tell us a lot about mycelial morphology, as it relates to the hyphal growth unit length, G, which can also be expressed as a volume. Observation of living cultures has shown that temperature increases do not affect G in some species. However, paramorphogens have been identified that do alter this ratio and hence G is linked to morphology.

In our vector based Neighbour-Sensing mathematical model, the inclusion of tropism vectors is also able to alter the E/μ ratio by affecting the parameter E, and this results in a striking array of different morphologies, some of which seem to suggest a morphogenetic process that goes beyond mycelial growth and towards differentiated tissues.

We will show you some of these in the next two pages and hope to convince you that the Neighbour-Sensing model represents real progress in modelling (and therefore understanding) key morphogenetic processes in fungi.

Copyright © David Moore 2017