Curvature compensation in the gravitropically bending Coprinopsis cinerea stem and the concepts of local curvature and local perception
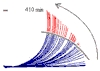
A schematic illustration of the curvature compensation reaction (which we have also called straightening) is shown in the diagram immediately below. After being turned to the horizontal position, the gravitropic bending process begins quite close to the apex. However, well before the apex reaches the vertical position, the apical part begins to straighten.
 |
| During the bending process the straightening progresses in the basipetal direction. When the stem is restored to the vertical in the final stages of the gravitropic reaction, most of the curvature is concentrated near the base (and the part which bent first is now straight). |
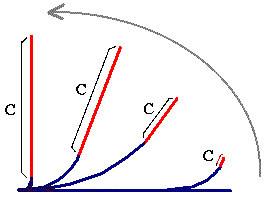
The illustration immediately below shows actual experimental data for Coprinopsis cinerea stems. The straight part is marked in red and separated from the rest by a grey line.
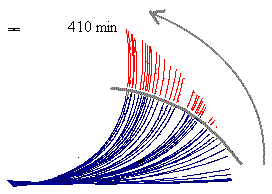 |
| The lengths of several replicate stems was normalised to 1 to generate mean values and the error bar for the experimentally observed data is displayed at top left. Computer-based image analysis was used to extract these data from video recordings. Statistical analysis indicates that the straightening process also occurs in more basal sections. |
The following diagram indicates how the curvature of the stem can be defined through the local angle (αL), curvature (CL), distance from the stem base (λ) and x and y co-ordinates of the point of interest.
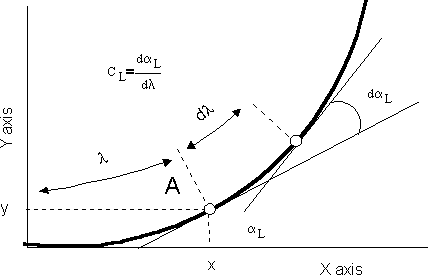 |
| Curvature is a ratio, calculated using the formula shown in the top left quarter of the figure. It is true as dλ tends to zero. The parameter dαL is mathematically defined as the angle of contingence. All parameters illustrated are for the point A. |
Some dependencies that can be calculated from the model parameters for Coprinopsis cinerea stems are shown in the two panels below
For both panels, the vertical axis is given in percent of the maximal value that both perception functions (S, R) acquire in the horizontal position (zero degrees to horizontal) and both distribution functions (A, L) acquire in the apex (represented by zero on the horizontal axis)). The dashed lines show 95% confidence intervals.
 |
| Gravitropic perception in the apex (S) and the local perception (R) are shown as functions of the reorientation angle, which is apex angle for S and the local angle for R. |
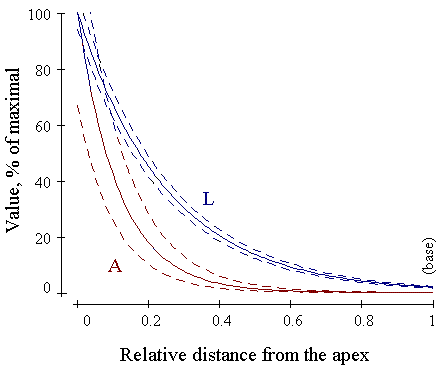 |
| Distribution of ability for local perception of the gravitropic signal (L) and straightening reaction (A) through the length of the stem. |
For further explanation see the following publications:
Meškauskas, A., Moore, D. & Novak-Frazer, L. (1998). Mathematical modelling of morphogenesis in fungi. Spatial organization of the gravitropic response in the mushroom stem of Coprinus cinereus. New Phytologist, 140: 111-123. [DOWNLOAD the PDF file of the published paper]
Meškauskas, A., Moore, D. & Novak-Frazer, L. (1999). Mathematical modelling of morphogenesis in fungi. 2. A key role for curvature compensation ('autotropism') in the local curvature distribution model. New Phytologist, 143: 387-399. [DOWNLOAD the PDF file of the published paper]
Close the window to return to your previous location
Copyright © David Moore, A. Meškauskas & L. Novak-Frazer 2017