2.2 Describing hyphal branching
Detailed observation by Katz et al. (1972) revealed that a germ-tube hypha will initially extend in length exponentially, at a rate that increases until a maximum, constant extension rate is reached, and that thereafter, it will increase in length linearly. The primary and subsequent branches will behave similarly. Thus, there develops a scenario in which individual hyphae extend linearly yet the biomass (or total length) of the whole mycelium increases exponentially. Trinci (1974) offered a solution to this paradox by proposing that it was due to the exponential increase in formation of hyphal tips due to branching.
In the same experiments, Katz et al. (1972) studied the growth kinetics of Aspergillus nidulans on three different media, each with a distinct specific growth rate. From this they were able to propose a number of general relationships that are conveyed in equation (1), elucidated by Steele & Trinci (1975):
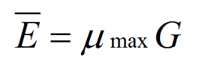 |
(1) |
where Ē is the mean tip extension rate, μmax is the maximum specific growth rate, and G is the hyphal growth unit. G is defined as the average length of a hypha supporting a growing tip according to equation (2):
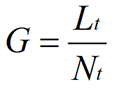 |
(2) |
where Lt is total mycelial length, and Nt is the total number of tips. The hyphal growth unit is approximately equal to the width of the peripheral growth zone, which is a ring-shaped peripheral area of the mycelium that contributes to radial expansion of the colony (Pirt, 1967; Trinci, 1971).
In a mycelium that is exploring the substratum, branching will be rare and thus G will be large. G is therefore an indicator of branching density; Katz et al. (1972) postulated that a new branch is initiated when the capacity for a hypha to extend increases above Ē, thereby regulating G ≈ 1 unit, the value of which is indicative of the branching density of that species of fungi on that particular medium.
For a range of fungi the hyphal growth unit increases following spore germination but then exhibits a series of damped oscillations tending towards a constant value (see top line in Figs 1 to 3 below). Such constancy demonstrates that over the mycelium as a whole, and not just in single hyphae, the number of branches is regulated in accord with increasing cytoplasmic volume. The hyphal growth unit is a length, measured in micrometres. Hyphal growth unit values have been measured for 21 fungal species, including both Zygomycota and Ascomycota that were cultured on a defined medium at 25°C; the values observed ranged from 35 to 682 µm with an average of 182 µm (Table 1).
Table 1. Lengths of hyphal growth units of a range of fungi grown on semi-solid glucose + mineral salts + vitamins medium at 25°C |
|||
|---|---|---|---|
| Zygomycota | Hyphal growth unit, G (µm) | Ascomycota | Hyphal growth unit, G (µm) |
| Actinomucor repens | 352 |
Botrytis fabae | 125 |
| Cunninghamella sp. | 35 |
Cladosporium sp. | 59 |
| Mucor hiemalis | 95 |
Fusarium avenaceum | 620 |
| Mucor rammanicinus | 37 |
Fusarium vaucerium | 682 |
| Rhizopus stolonifer | 124 |
Fusarium venenatum | 266 |
| Ascomycota | Geotrichum candidum | 110 |
|
| Aspergillus giganteus | 77 |
Neurospora crassa | 402 |
| Aspergillus nidulans | 130 |
Penicillium chrysogenum | 48 |
| Aspergillus niger | 77 |
Penicillium claviforme | 104 |
| Aspergillus oryzae | 167 |
Trichoderma viride | 160 |
| Aspergillus wentii | 66 |
Verticillium sp. | 82 |
Data from Bull & Trinci, 1977.
|
|||
The data in this table show that, on average, therefore, a 182 µm length of hypha is required to support extension of each hyphal apex.
This provision of resources for hyphal tip extension is visible cytologically as the flow of many vesicles (small vacuoles) towards the hyphal tip. A mathematical model has been created that produced numerical predictions of changes in total mycelial length, number of branches and distances between branches that compared well with observations of live fungi. This model assumes:
- vesicles are produced at a constant rate in distal hyphal regions;
- they are transported to the tip at a constant rate;
- at the hyphal tip vesicles accumulate and fuse with existing wall and membrane to give hyphal extension.
Bartnicki-Garcia (1973) proposed that hyphal tips extend by the incorporation into the tip membrane of new material that arrives packaged in vesicles supplied by a ‘vesicle supply centre’ (VSC). The concept is loosely based on the growth pattern described by Monod (1949) who, whilst studying bacterial growth, developed mathematical expressions of how a finite growth resource is translated into biological growth.
Resources Box The Monod Equation CLICK HERE if you would like to see a brief explanatory tutorial about the Monod equation |
A computer simulation model of the operation of the VSC was developed by Bartnicki-Garcia et al. (1989) and Riquelme et al. (2007) visualised the process in living hyphae of Neurospora crassa using chitin synthases labelled with green fluorescent protein.
To develop predictive algebraic models we need a foundation of quantitative observational data. Experimentally, we need to grow some mycelia and instead of simply observing, we need to measure the length of hypha formed, its rate of formation and how many branches arise. Let’s say we germinate a spore of on a medium providing all nutrients in excess and in sufficient volume to prevent any inhibitors accumulating. Then we count the number of hyphal tips and measure the total length of hypha produced. Some representative data are shown in Figs 1 - 3 below.
 |
|---|
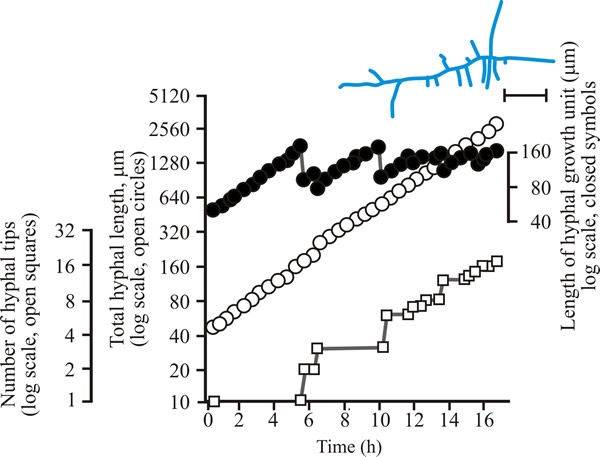
| Fig. 1. Initial growth of a mycelium of a spreading colonial mutant of Neurospora crassa on solid medium at 25°C. Open circles, total hyphal length produced by the germinating spore in µm; open squares, number of hyphal tips; solid circles, length of the hyphal growth unit in µm. The final appearance of the mycelium whose growth is recorded graphically is shown in the sketch at top right of the panel (scale bar = 250 µm). |
 |
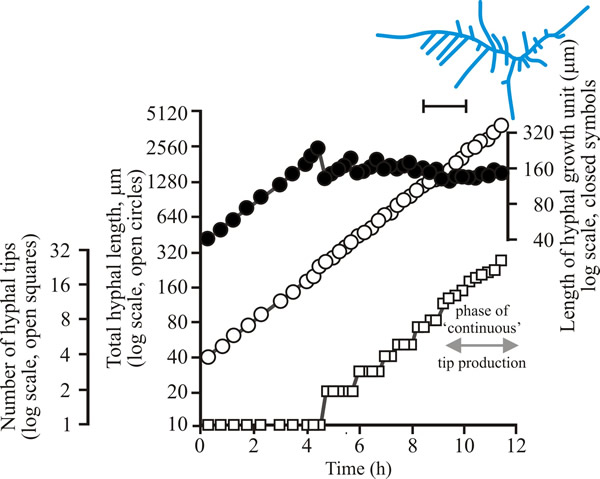
| Fig. 2. Initial growth of a mycelium of Aspergillus nidulans on solid medium at 25°C. Open circles, total hyphal length produced by the germinating spore in µm; open squares, number of hyphal tips; solid circles, length of the hyphal growth unit in µm. The final appearance of the mycelium whose growth is recorded graphically is shown in the sketch at top right of the panel (scale bar = 250 µm). |
 |
| Fig. 3. Initial growth of a mycelium of Geotrichum candidum on solid medium at 25°C. Open circles, total hyphal length produced by the germinating spore in µm; open squares, number of hyphal tips; solid circles, length of the hyphal growth unit in µm. The final appearance of the mycelium whose growth is recorded graphically is shown in the sketch at top right of the panel (scale bar = 250 µm). |
| Figs 1 to 3. Initial mycelium growth kinetics of young mycelia of Neurospora (Fig. 1), Aspergillus (Fig. 2) and Geotrichum (Fig. 3). Note that the graphs for both number of hyphal tips and total hyphal length become straight lines. As the vertical axis is logarithmic in these plots, this shows that these variables increase exponentially. Further, these two lines are eventually parallel so they must be increasing exponentially at the same rate. Evidently, ‘growth’, when measured in terms of total mycelial length, is exponential as a result of exponential branch formation. Total mycelial length and the total number of hyphal apices (all lead hyphae and branches) increase exponentially at the same specific rate. The hyphal growth unit is the mean length of hypha which contributes protoplasm to the extension of the tips of a mycelium, whilst the peripheral growth zone is the maximum length of hypha which contributes to the extension of the leading hyphal tips of a mature colony. In both cases the extension rate is a function of the length of hypha which contributes protoplasm to apical growth and of the organism’s specific growth rate. All illustrations modified and redrawn from Trinci, 1974. |
In all the examples shown in the panel above, note that the graphs for both number of hyphal tips and total hyphal length become straight lines. As the vertical axis is logarithmic in these plots, this shows that these variables increase exponentially. Further, these two lines are eventually parallel so they must be increasing exponentially at the same rate. Evidently, ‘growth’, when measured in terms of total mycelial length, is exponential as a result of exponential branch formation. Total mycelial length and the total number of hyphal apices (all lead hyphae and branches) increase exponentially at the same specific rate. This rate is equivalent to the specific growth rate of the organism under the same growth conditions in liquid medium, where biomass can be measured directly as dry weight.
We can express hyphal extension as a word model like this:
- during extension of a hypha, a new branch is initiated when the mean volume of cytoplasm per hyphal tip (we will call this the hyphal growth unit) exceeds a particular critical value;
- if the hyphal growth unit is ‘the mean volume of cytoplasm per hyphal tip’ it can be calculated as the ratio of total mycelial length to total number of hyphal tips.
Biologically the hyphal growth unit can be interpreted as the average volume of cytoplasm (equivalent to average length of hypha of uniform diameter) necessary to support the extension growth of a single average hyphal apex.
Prosser and Trinci (1979) used these premises in an algebraic model that successfully accounted for exponential growth and branching in fungal mycelia. The process was modelled in two steps:
- vesicles were produced in hyphal segments distal to the tip and were absorbed in tip segments;
- vesicles flowed towards the tip, moving from one segment to the next.
Apical branching initiated when the concentration of vesicles in the tip exceeded the maximum rate that the apex could absorb the new material. Varying the ratio of these steps produced different flow rates and branching patterns. The model also incorporated the concept of the ‘duplication cycle’ (Trinci, 1974). This was achieved by increasing the number of nuclei in the model mycelium at a rate proportional to the rate of biomass increase. Septa were then assumed to form in growing hyphae when the volume of the apical compartment per nucleus breached a threshold level. This provided for initiation of lateral branches by assuming that vesicles accumulated behind septa to a concentration comparable to that which initiated apical branching. This model achieved good agreement with experimental data for total mycelial length, number of hyphal tips, and hyphal growth unit length in Geotrichum candidum (Prosser & Trinci, 1979).
In an extension of this model, Yang et al., 1992a & b) used the concepts of vesicle production and the duplication cycle to account for hyphal growth and septation, respectively, in the deterministic element of a two-part model. They also included a stochastic element that accounted for the branching process whereby the branching site and the direction of branch growth were generated by probability functions. This gave rise to a much more realistic mycelial shape without compromising the agreement with experimental data for the parameters modelled by Prosser & Trinci (1979). Obviously a very close correspondence between theoretical predictions and real-life observations encourages the belief that the kinetic description of hyphal extension and branching we have given above is correct (Trinci et al., 1994, 2001).
Updated December 7, 2016
