4.4 Mycelium growth kinetics
One lesson to draw from the morphological description in the previous section is that the gross morphology can be very misleading. Systems that depend on outwardly directed extension, regular branching, and avoidance reactions (autotropism) can end up looking almost identical though they may not be related in any biological sense (for example a fungal mycelium compared with blood vasculature or with the growth of nerve fibres).
Evidently, from the description so far, in fungi there is an intimate relationship between hyphal extension rate, branch initiation and growth rate. Because of its importance to the understanding of the growth of filamentous fungi, it is essential to distinguish between ‘growth’ and ‘extension’:
- Growth (biosynthesis, or biomass production) occurs throughout a hypha,
- extension only occurs at the hyphal tip.
Thus, at the tip it is best to refer to hyphal extension rather than hyphal growth.
Eukaryotic hyphal organisms (members of kingdom Fungi and some Oomycota) can extend at very rapid rates because they have exploited the tactic of producing biomass, including membrane and cell wall precursors, over a long length of hypha subtending the extending tip (a 5 to 6 mm length in the case of Neurospora crassa) and rapidly transporting this biomass to the tip where the membrane and cell wall precursors are rapidly converted to new protoplasmic membrane and new cell wall. The rate at which new membrane and cell wall is added to the extension zone of a hypha and is then transformed into rigidified wall in N. crassa is quite remarkable considering it supports the extension growth mentioned above of 100 µm min-1 when grown at 37°C.
The basic features of fungal growth kinetics can be established with relatively straightforward experiments. A classic paper by Steele & Trinci (1975) showed that for a strain of N. crassa:
- there was a direct relationship between extension zone length and the rate of hyphal extension;
- extension zone length and hyphal diameter were not affected by temperature;
- at a particular temperature the extension zone expansion time (the time taken for a tip to expand from its minimum to its maximum diameter) was a constant (less than 60 sec).
These experiments indicated that at 25°C only seconds elapse between cell wall precursors of Neurospora crassa being added to the plastic extension zone of the wall at the tip and these materials being transformed into rigidified hyphal wall. Not all fungal species achieve such rapid rates of wall rigidification; hence the wide variation in the maximum rates of extension of fungal hyphae.
When growth rate is unaltered but extension rate is decreased (for example, by inclusion of inhibitory metabolite analogues like L-sorbose or validamycin A in the medium), newly synthesised biomass must be redirected towards increased branch formation. The important point here is that we are distinguishing between growth rate (as the rate in increase of biomass, which should strictly be called the specific growth rate) and the extension rate (the rate at which the colony margin marches across the substratum).
It’s fairly obvious that if the mycelium makes a lot of biomass but the hyphal tips do not extend by an equivalent amount then the biomass must go somewhere and the only place it can go is into more branches. This is the verbal description of the kinetic equation that describes a mycelium that is exploiting a resource (it also, incidentally, describes the ‘make a fruit body’ situation if you also add a reversal of the normal autotropism so that the branches can cluster together rather than grow away from each other).
The contrasting situation consists of a rapidly-extending mycelial margin, in which the majority of the biomass is devoted to driving the hyphal tip extension with very little branching. Here again you can readily understand that if the mycelium is making more biomass but is not making many branches then the extension rate of the mycelial margin must increase. For the moment these are theoretical interpretations based on visual observation. What we’ve done so far is create a model of hyphal growth in words. It’s pretty powerful, in that it seems capable of explaining quite a lot, but it is just a word model, so how can we establish if it represents the truth? To enable statistical testing we need some numbers so we can convert this into a mathematical model.
We need to grow some mycelia and instead of simply observing, we need to measure the length of hypha formed, its rate of formation and how many branches arise. Let’s say we germinate a spore of on a medium providing all nutrients in excess and in sufficient volume to prevent any inhibitors accumulating. Then we count the number of hyphal tips and measure the total length of hypha produced. Some representative data are shown in Figs 7 - 9.
 |
|---|
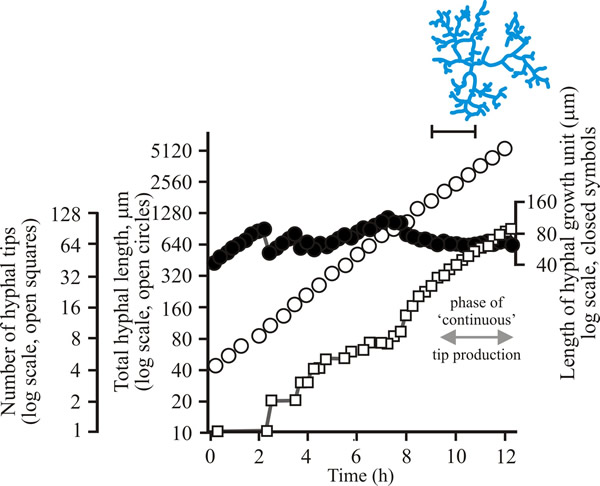
| Fig. 7. Initial growth of a mycelium of a spreading colonial mutant of Neurospora crassa on solid medium at 25°C. Open circles = total hyphal length produced by the germinating spore in µm; open squares = number of hyphal tips; solid circles = length of the hyphal growth unit in µm. The final appearance of the mycelium whose growth is recorded graphically is shown in the sketch at top right of the panel (scale bar = 250 µm). |
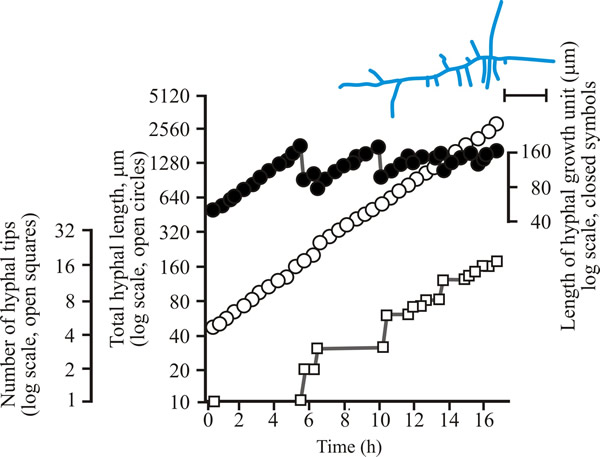 |
| Fig. 8. Initial growth of a mycelium of Aspergillus nidulans on solid medium at 25°C. Open circles = total hyphal length produced by the germinating spore in µm; open squares = number of hyphal tips; solid circles = length of the hyphal growth unit in µm. The final appearance of the mycelium whose growth is recorded graphically is shown in the sketch at top right of the panel (scale bar = 250 µm). |
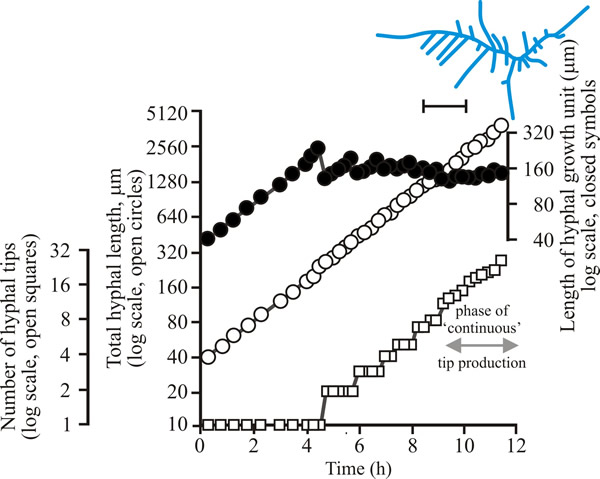 |
| Fig. 9. Initial growth of a mycelium of Geotrichum candidum on solid medium at 25°C. Open circles = total hyphal length produced by the germinating spore in µm; open squares = number of hyphal tips; solid circles = length of the hyphal growth unit in µm. The final appearance of the mycelium whose growth is recorded graphically is shown in the sketch at top right of the panel (scale bar = 250 µm). |
| Figs 7 to 9. Initial mycelium growth kinetics of young mycelia of Neurospora (Fig. 4.7), Aspergillus (Fig. 4.8) and Geotrichum (Fig. 4.9). Note that the graphs for both number of hyphal tips and total hyphal length become straight lines. As the vertical axis is logarithmic in these plots, this shows that these variables increase exponentially. Further, these two lines are eventually parallel so they must be increasing exponentially at the same rate. Evidently, ‘growth’, when measured in terms of total mycelial length, is exponential as a result of exponential branch formation. Total mycelial length and the total number of hyphal apices (all lead hyphae and branches) increase exponentially at the same specific rate. The hyphal growth unit is the mean length of hypha which contributes protoplasm to the extension of the tips of a mycelium, whilst the peripheral growth zone is the maximum length of hypha which contributes to the extension of the leading hyphal tips of a mature colony (Fig. 4.13). In both cases the extension rate is a function of the length of hypha which contributes protoplasm to apical growth and of the organism’s specific growth rate. All illustrations modified and redrawn from Trinci, 1974. |
In all these examples, note that the graphs for both number of hyphal tips and total hyphal length become straight lines. As the vertical axis is logarithmic in these plots, this shows that these variables increase exponentially. Further, these two lines are eventually parallel, so they must be increasing exponentially at the same rate. Evidently, ‘growth’, when measured in terms of total mycelial length, is exponential because of exponential branch formation. Total mycelial length and the total number of hyphal apices (all lead hyphae and branches) increase exponentially at the same specific rate. This rate is equivalent to the specific growth rate of the organism under the same growth conditions in liquid medium, where biomass can be measured directly as dry weight.
We can refine our word model now to this:
- during extension of a hypha, a new branch is initiated when the mean volume of cytoplasm per hyphal tip (we will call this the hyphal growth unit) exceeds a particular critical value.
- If the hyphal growth unit is ‘the mean volume of cytoplasm per hyphal tip’ it can be calculated as the ratio of total mycelial length to total number of hyphal tips.
Biologically the hyphal growth unit can be interpreted as the average volume of cytoplasm (equivalent to average length of hypha of uniform diameter) necessary to support the extension growth of a single average hyphal apex.
For a range of fungi the hyphal growth unit increases following spore germination but then exhibits a series of damped oscillations tending towards a constant value (see top line in Figs 7 to 9). Such constancy demonstrates that over the mycelium as a whole, and not just in single hyphae, the number of branches is regulated in accord with increasing cytoplasmic volume. The hyphal growth unit is the population parameter which describes this. The hyphal growth unit is a length, measured in µm. Hyphal growth unit values have been measured for 21 fungal species, including both zygomycetes and Ascomycota that were cultured on a defined medium at 25°C; the values observed ranged from 35 to 682 µm with an average of 182 µm (Table 1).
Table 1. Lengths of hyphal
growth units of a range of fungi grown on semi-solid glucose+mineral
salts+vitamins medium at 25°C |
|||
|---|---|---|---|
| Zygomycota | Hyphal growth unit, G (µm) |
Ascomycota | Hyphal growth unit, G (µm) |
| Actinomucor repens | 352 |
Botrytis fabae | 125 |
| Cunninghamella sp. | 35 |
Cladosporium sp. | 59 |
| Mucor hiemalis | 95 |
Fusarium avenaceum | 620 |
| Mucor rammanicinus | 37 |
Fusarium vaucerium | 682 |
| Rhizopus stolonifer | 124 |
Fusarium venenatum | 266 |
| Ascomycota | Geotrichum candidum | 110 |
|
| Aspergillus nidulans | 130 |
Neurospora crassa | 402 |
| Aspergillus giganteus | 77 |
Penicillium chrysogenum | 48 |
| Aspergillus oryzae | 167 |
Penicillium claviforme | 104 |
| Aspergillus niger | 77 |
Verticillium sp. | 82 |
| Aspergillus wentii | 66 |
Trichoderma viride | 160 |
Data from Bull & Trinci, 1977.
|
|||
On average, therefore, across this range of fungi a 182 µm length of hypha is required to support extension of the hyphal apex. As we will see later, provision of resources for hyphal tip extension is visible cytologically as the flow of many vesicles (small vacuoles) towards the hyphal tip. A mathematical model has been created that produced numerical predictions of changes in total mycelial length, number of branches and distances between branches that compared well with observations of live fungi. This model assumes:
- vesicles are produced at a constant rate in distal hyphal regions,
- they are transported to the tip at a constant rate,
- at the hyphal tip vesicles accumulate and fuse with existing wall and membrane to give hyphal extension.
Obviously a very close correspondence between theoretical predictions and real life observations encourages the belief that the description we have been giving is correct (Trinci et al., 1994, 2001).
Updated July, 2019
