Experimental observations on the spatial organisation of the gravitropic curvature

Experimental observations of disoriented stems of the small ink cap mushroom, Coprinopsis cinerea, provided the foundation for development of all the mathematical models discussed in these pages.

The purpose of the work done for this specific model was to establish how the distribution  of local curvatures changed during the mushroom stem's gravitropic reaction and to suggest a suitable mathematical description based on these new data.

The gravitropic bending of base- and apex-pinned Coprinopsis cinerea stems was recorded on videotapes (at that time the organism was called Coprinus cinereus (Fries) S. F. Gray). The video images were captured from the tapes at 10 minute intervals and digitised using a computer fitted with a dedicated videoimage analysis card. The image analysis card then transformed the digital images into tables of co-ordinates of points for each stem, at each sampled time point.

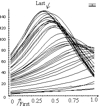
Non-linear regression of these data was performed using Legendre polynomials. From the resulting equations the patterns of changing local curvature for 50 subsections of each stem during 400 min of gravitropic reaction were calculated and replicates combined statistically to obtain an understanding of the average behaviour of the population of 14 independent replicate stems. A sample of the observations is shown in Figure 1.

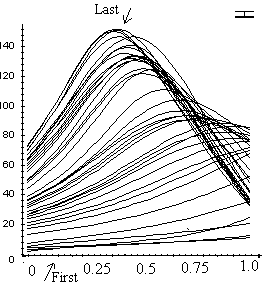Figure 1. The distribution of local curvature over  the length of the stems of Coprinopsis cinerea pinned to a horizontal platform through their base. Curves represent sets of observations made at 10-minute  time intervals. Vertical axis shows local curvature in angular degrees; Replicate stems varied slightly in length and were normalised to a the same overall length (= 1.0) so the horizontal axis shows the relative distance from the base of each of the 50 subsections calculated for each stem. Distance from the base (position zero) is given in arbitrary units of the normalised stem length. The error bar at top right represents the maximal standard deviation of the set of replicates used for the figure.

It was observed that base-pinned stems first bent from the apex, but later the curvature of this part decreased, and in the late stages the apex became nearly completely straight again. Subsections located about one third of stem length from the base determined the main part of the final upward curvature.

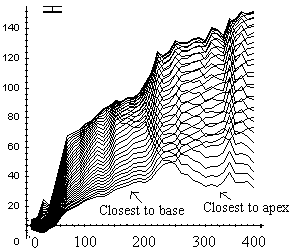Figure 2. The   distribution of  local  curvature over  the length of the stem for base-pinned C. cinerea stems.  Each curve represents the changing  curvature of a different stem subsection. Error  bar at top left represents maximal standard deviation.  Vertical axis shows local curvature in angular degrees; the horizontal axis shows the elapsed time in minutes (time zero = time when the stem was reoriented from vertical to horizontal).

The free basal part of the apex-pinned stems bent upward, and after a certain bending time also began to straighten (Figure 3). However, this process started significantly later and was weaker than in base-pinned stems. Bending of the subsections close to the pinned apex did not stop when the stem reached the vertical position (remember in apex-pinned stems it was the stem base that was being lifted to the vertical), and the final angle of gravitropic curvature of these stems could exceed 180°.

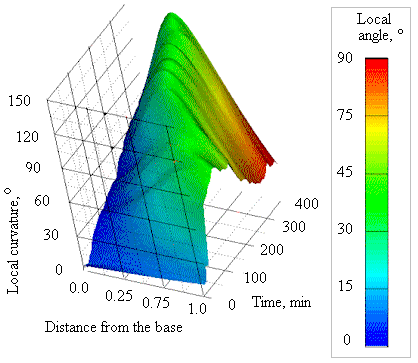Figure 3. Surface, generated  by Maple Software [view website], describing the development of the gravitropic curvature in apex-pinned Coprinopsis cinerea stems. Distance from the base is given in arbitrary units of stem length as replicates were normalised, base = zero, apex = 1.0. The surface shown represents the curvature of the 50 subsections of stem (average over all replicates) in angular degrees with the absolute value of the local angle of each subsection colour-coded (spectrum scale bar at right).

Plotting various functions of local bending speed and its derivatives against each other and against local angle indicated that, if the hypothetical signal for reorientation arises in the apex, its propagation towards the base did not follow simple wave or simple diffusion laws.

The importance of the local angle of all subsections both for signal origin and transmission was established and a signal transmission equation, involving local angle of each subsection, was derived. After creating a suitable program this partial differential equation was solved numerically. The simulated shapes of the bending stem coincided almost exactly with experimentally observed images.

For details, see Meskauskas, A., Moore, D. & Novak-Frazer, L.(1998). Mathematical modelling of morphogenesis in fungi. Spatial organisation of the gravitropic response in the mushroom stem of Coprinus cinereus. New Phytologist, 140: 111-123. Download the PDF

Close the window to return to your previous location