2.5 Tropism and Hyphal Interactions
While it is significant that a purely stochastic approach can generate realistic colony morphology, this does not mean that tropism and hyphal interactions are irrelevant to modelling hyphal growth. Hyphae certainly do use autotropic behaviour (positive and negative) to control spatial organisation in particular regions of the mycelium. Where the hyphal density is high, as in fungal tissues, interactions are inevitable.
Edelstein (1982) was the first to consider such interactions. Her approach differed in that instead of considering the mechanisms of growth in discrete hyphae, she looked at the mycelium as a whole. She assumed that growth occurred at a constant rate throughout the mycelium. This she set at μmax and so also limited her model to a tangential abstraction of the growth curve. Her model owes something to Cohen (1967) in that it considers the density of the mycelium with respect to space as a key feature. Two density parameters were defined:
- p = p(x,t) the hyphal density per unit area;
- n = n(x,t) the tip density per unit area;
and the model was then based on two partial differential equations:
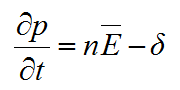 |
(17) |
 |
(18) |
where δ = δ(p) is the rate of hyphal death, σ = σ(n,p) is the rate of tip creation, and nĒ can be considered as tip flux.
Edelstein (1982) also defined, in mathematical terms, all the hyphal interactions that affect the parameter n, and which are contained in the function σ. These included branching mechanisms, as well as tip death and tip-tip and tip-hypha anastomoses.
She then used phase plane analysis to determine which of various combinations of hyphal interactions, expressed mathematically in the function σ, had bounded non-negative solutions of equations (17) and (18). These represented combinations that yielded spatially propagating colonies. Her results showed that when δ = 0, only colonies that branched dichotomously and formed tip-hypha anastomosis could propagate. However, when δ > 0, most combinations of hyphal interactions yielded propagating colonies. Thus, hyphal death was an important feature of mycelial growth.
Ferret et al. (1999) adopted a similar approach to Edelstein (1982), using two partial differential equations that considered parameters defined in dimensions of density. However, they sought to apply the model macroscopically by adjusting Ē (mean tip extension rate ) with respect to X. This was done by collecting data that quantified how E varied when two hyphae came into close proximity with each other. This effect was incorporated into the differential equation concerned with the rate of change of biomass density (proportional to hyphal-density) so that it was more likely to be applied in regions where the density of biomass was high, and had a greater effect on regions where the density of tips was high. Thus, Ē decreased as the mycelium grew and biomass increased.
This approach provides an alternative to incorporating hyphal death into the model that has the advantage of also affecting Ē, thus limiting growth in a manner typical of batch culture. This limiting mechanism is an approximation however, as the true limiting parameter for biomass evolution is specific growth rate (see equation (5)). In reality, μ can decrease as hyphae die, whereas the mean extension rate of the remaining hyphae can be maintained despite overall biomass evolution slowing.
The rate of change of tip density was determined with respect to a diffusion coefficient that was dependent on temperature and medium conditions. This offered a means of modelling the affect of changing environmental conditions on macroscopic growth kinetics when only microscopic parameters had been measured. The value of this parameter was estimated from experimental data and gave comparable results when used in the mathematical model. This was validated further by the agreement between experimental and simulated data on the width of the peripheral growth zone, even though this parameter was not included in the initial design of the model.
Updated December 7, 2016
